An Improved Staggered Double Vane Slow Wave Structure and Its Interaction Structure Working on TE30 High-order Mode
-
摘要:
随着行波管的工作频段不断向太赫兹频段发展,尺寸共渡效应的影响越来越明显,主要表现为慢波结构的横向尺寸和电子注通道的宽度不断减小,不仅造成了加工工艺难度的提升,也导致了工作电流的减小以及耦合阻抗的下降,严重影响了行波管性能,而工作在高次模式的过模行波管能有效解决这一问题。文中研究了过模交错栅的工作特性,并针对低次模式竞争及返波振荡等问题,提出了一种改进型交错栅。该结构工作在高次TE30模式,相比于同频段工作在基模的电路,其横向尺寸和电子注通道高度分别扩展了3倍和2倍。模式分析的结果表明,新结构在相对较低的工作电压下能够有效抑制返波振荡和模式竞争。基于新型结构设计了两段式高频电路。PIC仿真表明,在26 kV电压、两个150 mA带状注的工作条件下,在217 GHz频率上可以获得103.5 W的功率输出,增益为19.6 dB,频谱分析结果表明工作稳定,无振荡发生。该工作对过模行波管的研制具有指导意义。
Abstract:As the operating frequency band of traveling wave tubes continues to advance into the terahertz frequency band, the influence of the size co-transit effect is becoming more and more obvious, which is mainly manifested in the continuous reduction of the transverse size of the slow wave structure and the width of the electron beam channel, resulting in the improvement of the processing difficulty, the reduction of the operating current and the decrease of the coupling impedance, which seriously affects the performance of the traveling wave tubes. Over-mode traveling wave tubes operating in higher order mode can solve this problem effectively. In order to solve the problems of low-order mode competition and back-wave oscillation, an improved staggered double vane slow wave structure is proposed. This structure works in high-order TE30 mode. Compared with the basic mode circuit operating in the same frequency band, the transverse size and channel height are extended by 3 times and 2 times, respectively. The results of mode analysis show that the new structure can effectively suppress back-wave oscillation and mode competition at relatively low operating voltage. Based on the new structure, a two-stage high frequency circuit is designed. PIC simulation shows that the power output of 103.5 W can be obtained at 217 GHz with a gain of 19.6 dB at 26 kV voltage and two 150 mA sheet-beams. The spectrum analysis results show that the operation is stable and no oscillation occurs. This work has guiding significance for the development of over-mode traveling wave tubes.
-
Keywords:
- terahertz /
- over-mode /
- dimensional co-transit effect /
- slow wave structure /
- back-wave oscillation
-
0. 引言
太赫兹波一般指的是频率在100 GHz~10 THz范围的电磁波,由于其具有高频率、大带宽、保密性好等特点,在高速通信[1-2]、医疗、航空航天等领域具有广泛的应用价值。太赫兹低频段220 GHz刚好在大气窗口的光谱范围内,电磁波传播损耗较小,具有较高的研究价值。
然而,在行波管工作频段逐渐向太赫兹频段发展的过程中,随着器件尺寸的减小,尺寸共渡效应的影响愈发明显。尺寸共渡效应是指在行波管的工作频率提高的过程中,慢波结构的横向尺寸和电子注通道的宽度会不断减小,这一方面造成了加工工艺难度的提升和工作电流的减小;另一方面,频率的升高使表面波的衰逝速度加快,造成了电子注流通区域内变得很弱,导致注波互作用程度减弱,造成慢波结构的耦合阻抗很小,进而使得互作用效率下降[3]。工作在高次模式的过模行波管,由于高次模式场分布的特点,具有更大的横向尺寸,且能够适应高电压、大电流的输入,以TE30模过模行波管为例,其横向尺寸约为同频段基模行波管的3倍,能够有效地降低加工工艺的难度,同时能够通过更大的电流,为提高输出功率创造条件。
过模行波管的主要问题是会引起低次模式前向波的模式竞争以及反波振荡[4]等问题,从而导致输出功率和增益受到限制。目前过模行波管常用的抑制以上问题的技术有介质加载,脊/槽加载,以及在电子注通道中间加入矩形金属柱完全隔绝相邻通道。
从国内外已有的研究结果来看,现有的过模行波管大致分为两类:一类在抑制低次模式的同时输出功率也受到了限制[5-6];另一类有较高的增益和输出功率,但其工作电压高达50 kV以上[3, 7],匹配的电子枪及磁聚焦系统难以实现。近年来,在交错栅及正弦波导类型的过模慢波结构的研究中,采用在电子注通道中间加入矩形金属柱的返波振荡抑制的研究较多[8-9],不可否认该方法确实是一种提高太赫兹行波管输出功率的有效手段。但采用这种技术的慢波结构,其高次模式的色散曲线几乎与基模重合,且该结构在物理模型上与相邻电子注通道完全隔绝,从色散曲线和物理结构上来看,这种类型的慢波结构更类似于并排的基模多注行波管,只具有小部分过模特性。在不影响过模特性的前提下,文中在传统交错栅类慢波结构的基础上提出一种适合工作在高次模式的慢波结构。
文中第1节给出了新结构模型,并将其冷测特性与传统TE30模式交错栅进行了对比,证明了其更适合过模工作并对机理进行了分析。第2节对该结构的两段电路进行了注波互作用仿真,在未加入损耗介质的情况下实现了较好的输出结果,与冷测特性相印证。
1. 结构参数及冷测特性仿真
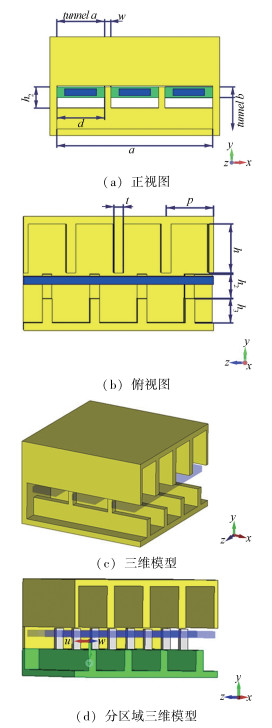
图 1为提出的新型交错栅慢波结构。其结构参数如表 1所示。其中,a为结构整体宽度;p为周期长度;t为单侧栅沿传播方向的长度,同时也是齿沿传播方向的长度;h为长栅长度;d为齿间距;w为齿的横向宽度;h2为齿的长度;h3为短栅长度;tunnel a和tunnel b分别为电子注通道在横截面上的宽度和高度。
表 1 新结构参数
该结构在沿传播方向的纵向上分为三个区域:上半部分为加长的经典单侧栅(图 1(d)中黄色部分);中间区域为沿横向三等分的齿状结构,齿的长度为长栅的一半(图 1(d)中银色部分);图 1(d)中蓝色部分为电子注[10],从齿的缝隙中穿过,电子注通道高度为齿的1/2;下半部分为较短的经典单侧栅,长度为长栅的一半(图 1(d)绿色部分)。根据后续章节1.1.1该结构TE30模式场分布的特点,通道处上半部分TE30模式电场能量较高,下半部分工作模式电场能量较低,且返波电场能量较高,很容易引起返波振荡,因此选取通道的一半作为电子注道。
从几何模型上来看,改进后的交错栅在横向尺寸和电子注通道高度上分别为同频段基模交错栅的3倍和2倍,大大降低了制造工艺的难度。同时,中心通道的高度有了较大提升,虽然只有上半部分通道能够进行有效的互作用,但整体较宽的通道也有利于解决慢波结构的散热问题。
1.1 新结构冷测特性及场分析
改进后的新结构不仅具有尺寸上的优势,而且其冷测特性也与传统的TE30模交错栅有所不同,主要表现在场分布上竞争模式及返波的电场能量大大降低,色散曲线上各个模式的频率-相位曲线变得更为“分散”,耦合阻抗整体上得到了一定提升且具有了一种新的特性。
1.1.1 场分布
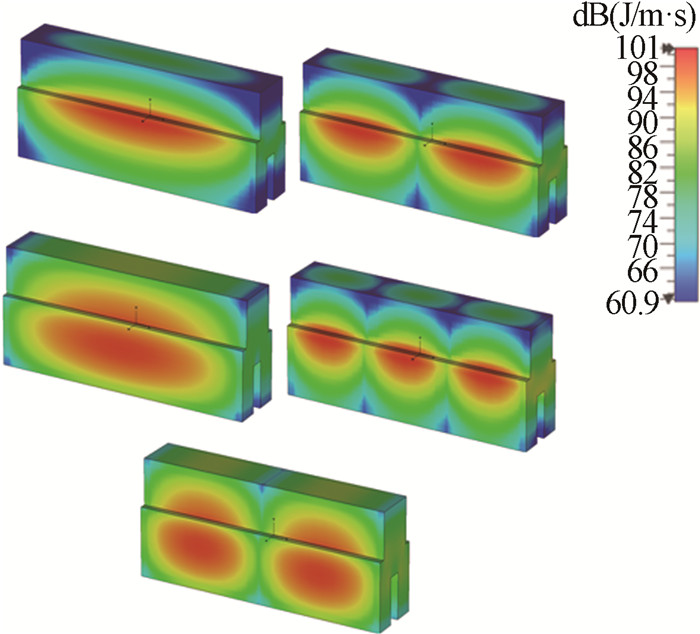
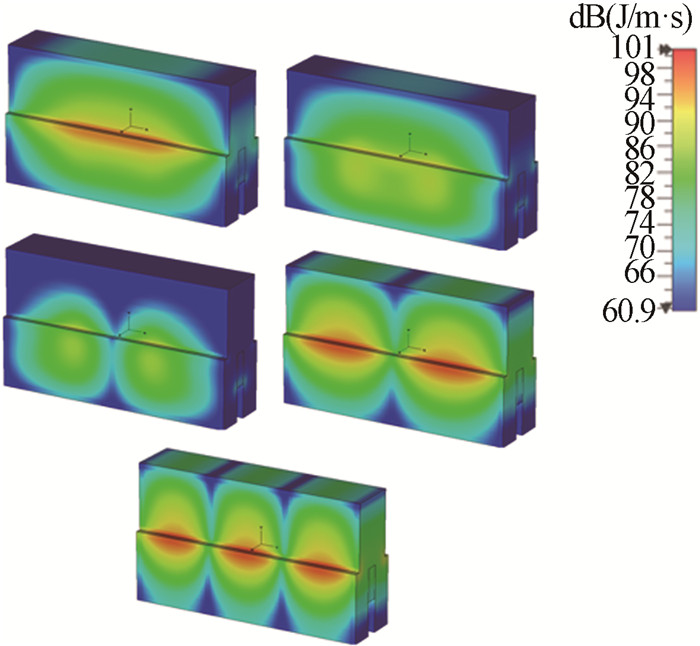
图 2和图 3分别为通过CST本征模求解器得出的传统TE30模交错栅电场能量分布图和改进后的结构电场能量分布图。
可以看出,相比于传统的过模交错栅,改进后的结构的低次模式及返波的电场能量大大降低,且这些模式中心区域分布范围大大减小,说明该结构对低次模式及返波抑制效果较好。
1.1.2 色散特性
色散特性可以表征慢波结构的带宽、相速、群速以及模式之间禁带等基本信息,根据色散特性可以确定行波管的工作模式和电子注电压,对慢波结构的仿真具有重要意义。文献[8]中给出了传统交错双栅慢波结构的色散曲线理论推导过程,其解是一个极为复杂的形式,改进后的新结构相比于传统交错双栅慢波结构更为复杂,对其进行场论分析时要分成十几个区域进行讨论,色散曲线的求解更为复杂,这里暂不做推导。通过CST本征模求解器计算出新结构的色散曲线。
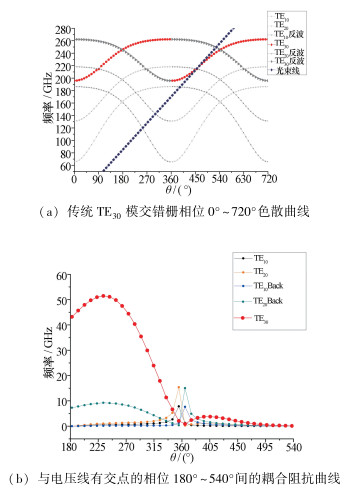
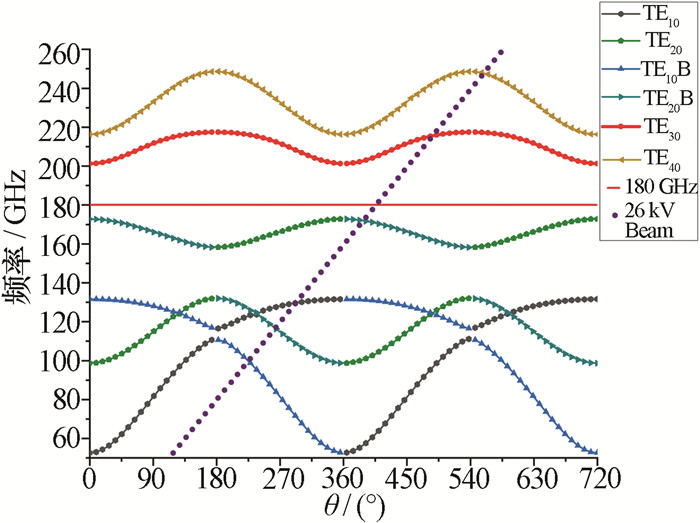
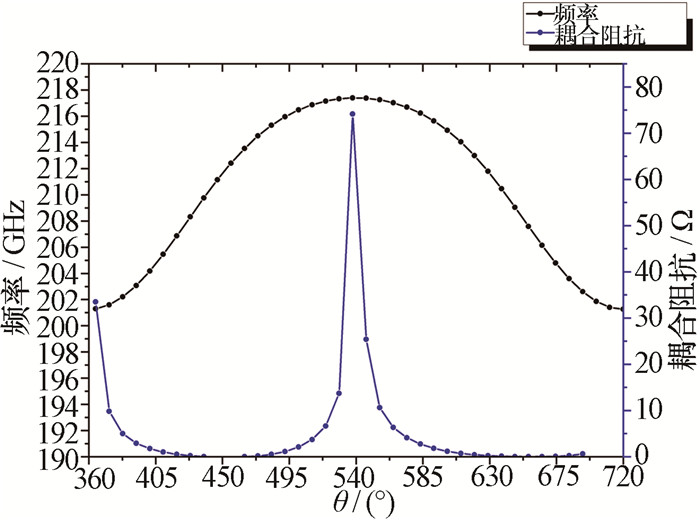
图 4为传统TE30模交错栅相位0°~720°色散曲线及与电压线有交点的相位180°~540°间的耦合阻抗曲线,图 5为新结构各个模式色散曲线,其中红色曲线为TE30模式,26 kV电压线与其穿过的模式的交点处的频率及耦合阻抗如表 2所示。图 6为归一化相速度曲线,根据该曲线可计算出慢波结构的匹配电压约为26 kV。
表 2 26 kV电压线交点处各模式频率及耦合阻抗模式 10返波 20返波 10前向波 20返波 30工作点 谐波次数 -1 -1 -1 0 0 频率/GHz 101.00 117.00 129.50 171.00 217.32 耦合阻抗/Ω 0.37 0.60 5.20 2.57 15.60 相比于传统TE30模交错栅,新结构的竞争模式及返波耦合阻抗很低,而工作模式在工作点处有较高的耦合阻抗,这与前文电场能量分布的结果相吻合。
将图 4与图 5进行对比可以发现,新结构的色散曲线虽然可用带宽变窄了,但是各个模式之间变得更为“分散”,这种变化带来了两个好处:一是低次模式及其返波的频率被压在了更低的区域,与文中的工作模式TE30模有很大距离,这样就可以通过光子晶体加载[9-10]以及其他频率选择性的衰减技术完全消除低次模式;二是电压线与低次模式交点离工作点更远,与传统TE30模交错栅相比,电压线交点处的耦合阻抗大大降低,减小了模式竞争及返波振荡的可能。
除此之外,从图 5可以看出,对于新结构,在TE30模以下的模式中,色散曲线在不同程度上被“切断”,相比之下,TE30模式受到的影响较小,几乎与传统交错栅一致,TE30模式受到的影响更为明显,其色散曲线产生了一个很大的禁带;此外,TE30模及比其更高次的模式周期缩小为传统过模交错栅的一半,导致原本的CST中前向波和返波为两条曲线,现在合成了一条,这带来了耦合阻抗上的一些变化,将在下一小节具体说明。
1.1.3 耦合阻抗
耦合阻抗反映了荷电粒子与电磁波相互作用的程度, 而荷电粒子通常沿通道纵向运动, 因此与荷电粒子发生互作用的通常是电场的纵向分量。根据耦合阻抗的定义[11],慢波结构中n次空间谐波的耦合阻抗为
$$ K_{\mathrm{c}n}=\frac{E_{z n} E_{z n}^*}{2 \beta_n^2 P_z} $$ (1) 式中:Ezn为电子束位置处第n次空间谐波的电场纵向分量;Pz为沿轴向传输的总的高频功率流;βn表示第n次空间谐波在z方向的波数,βn =β0 +2nπ/p,β0为基波纵向波数。
可以使用CST软件的本征模求解器求解Ezn和Pz,但需要将定义式分解为CST中的基本物理量, 根据傅里叶周期展开的特性,有
$$ \begin{aligned} E_{z n}= & \frac{1}{p} \int_0^p E_z(x, y, z) \mathrm{e}^{\mathrm{i} \beta_n z} \mathrm{d} z= \\ & \frac{1}{p} \int_0^p\left[\operatorname{Re}\left(E_z\right) \cos \left(\beta_n z\right)-\operatorname{Im}\left(E_z\right) \sin \left(\beta_n z\right)\right] \mathrm{d} z+ \\ & \left.\mathrm{j} \frac{1}{p} \int_0^p\left[\operatorname{Re}\left(E_z\right) \sin \beta_n z\right)+\operatorname{Im}\left(E_z\right) \cos \left(\beta_n z\right)\right] \mathrm{d} z \\ E_{z n} E_{z n}^* & =\left|E_{z n}\right|^2= \\ & \quad \left\{\int_0^p\left[\operatorname{Re}\left(E_z\right) \cos \left(\beta_n z\right)-\operatorname{Im}\left(E_z\right) \sin \left(\beta_n z\right)\right] \mathrm{d} z\right\}^2+ \\ & \quad \left\{\frac{1}{p} \int_0^p\left[\operatorname{Re}\left(E_z\right) \sin \left(\beta_n z\right)+\operatorname{Im}\left(E_z\right) \cos \left(\beta_n z\right)\right] \mathrm{d} z\right\}^2 \end{aligned} $$ (2) 将坡印廷矢量的z分量在横截面积分可得Pz,在CST本征模求解器中进行后处理可得出耦合阻抗曲线。
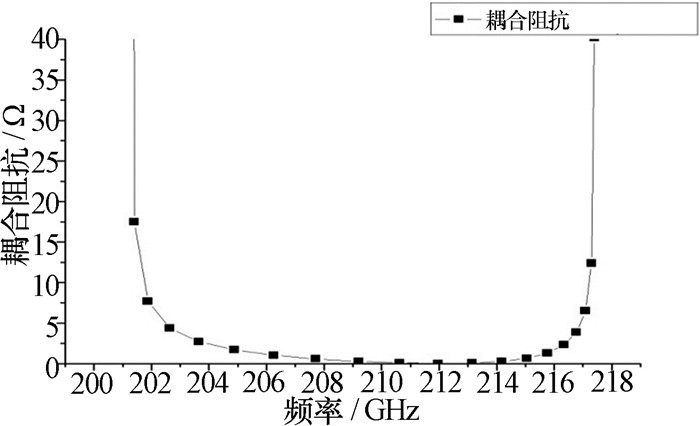
从图 2和图 3的电场能量分布图可以看出,新结构中心通道处TE10模式电场较强且与TE30模式电场区域重复很难抑制,因此选取两侧通道作为互作用区域并计算其耦合阻抗。新结构在360°~720°相位之间的耦合阻抗随相位变化曲线如图 7所示,图中黑色曲线代表TE30模式色散曲线,蓝色曲线代表TE30模式耦合阻抗随相位的变化。图 8为该区间耦合阻抗随频率变化的曲线。图 7中前半段(360°~450°)相位区间新结构耦合阻抗变化规律符合常见的前向波的耦合阻抗,快速下降后趋于稳定;然而在后半段(450°~540°)相位区间内,耦合阻抗先是缓慢增加,接近540°相位时急剧增加,最高点处甚至高达70 Ω,本结构选择的工作点耦合阻抗在10 Ω以上,这将给TE30模式前向波在模式竞争中带来一定的优势,更有利于抑制低次模式竞争和返波振荡。并且结合图 6的归一化相速度曲线来看,行波管工作在450°~540°相位之间大大降低了归一化相速度,从而大大降低了匹配电压,在耦合阻抗不降反增的情况下解决了高增益过模行波管往往需要高工作电压的问题[12]。
2. 注-波互作用仿真
在冷测特性的基础上,本文在CST粒子工作室进行了注-波互作用仿真,从图 3的电场能量分布图可以看出,中心通道处TE10模式电场较强且与TE30模式电场区域重复很难抑制,多次PIC仿真的结果也表明在中心区域增加电子注极易引起TE30模式的模式竞争及返波振荡,因此暂时选取两侧通道作为互作用区域。但要注意的是,虽然中心区域没有添加电子注,但TE30模式的电场在横向上仍是一个整体,切断中心区域电场也会破坏两侧的电场,互作用将减弱甚至消失。
在此基础上,文中分别进行了新结构单段和两段电路的注-波互作用仿真,输入电压为26 kV,电子注采用两个150 mA的带状注,网格数量为3 325 608,激励信号采用217 GHz正弦信号。
2.1 模式竞争分析
由于单段电路增益较低,需要很大的输入信号才能输出较高的功率,加长单段电路虽然能有效提高增益,但是增加长度对返波的增益提高效果远远大于对前向波的增益提升,单段电路过长会导致严重的返波振荡,其原因如下:
已知行波管中的特征方程(此时C ≪ 1)
$$ \delta^2=\frac{1}{-b+\mathrm{j} d+\mathrm{j} \delta}-4 Q C $$ (3) 该方程有三个根,第四个根由于不参与注波互作用因此被忽略。这三个根分别代表:增幅波、衰减波与等幅波。在足够的互作用距离后,实际只需要考虑增幅波的变化情况。
通过考虑边界条件,可以求解出慢波线上任意点的高频电压
$$ \frac{V(z)}{V}=\mathrm{e}^{-\mathrm{j} 2 \mathtt{π} N} \sum\limits_{n=1}^3\left[\frac{\delta_n^2+4 Q C}{\left(\delta_n-\delta_{n+1}\right)\left(\delta_n-\delta_{n+2}\right)} \mathrm{e}^{2 z C N \delta_n}\right] $$ (4) 这里只需要把位置z替换为互作用长度l,并与z=0比对即可,分母的电压V被消掉,从而得到
$$ \frac{V(0)}{V(l)}=\frac{\sum\limits_{n=1}^3\left[\frac{\delta_n^2+4 Q C}{\left(\delta_n-\delta_{n+1}\right)\left(\delta_n-\delta_{n+2}\right)}\right]}{\sum\limits_{n=1}^3\left[\frac{\delta_n^2+4 Q C}{\left(\delta_n-\delta_{n+1}\right)\left(\delta_n-\delta_{n+2}\right)} \mathrm{e}^{2 z C N \delta_n}\right]}=\infty $$ (5) 这就是产生振荡的根本原因:当发生振荡时,能量被反馈回输入端口并且相比于输入信号被放大了无穷倍。虽然在理想条件下计算是无穷值,但实际上两个信号的能量差一个数量级时就会产生明显的振荡现象。而互作用长度l位于分母的指数次位置,单段电路l的增加会导致返波振荡的可能大幅增加。因此要让单段电路稳定工作就需要一个适当的互作用长度,经过多次仿真最终选择30个周期长度的单段电路。
2.2 单段电路仿真结果
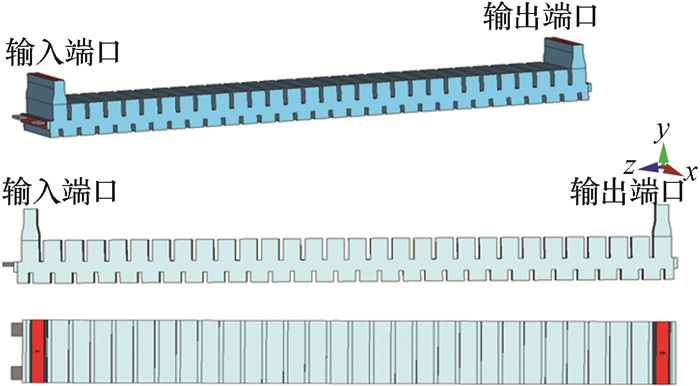
首先对单段长度为30个周期的电路进行了仿真,单段电路模型如图 9所示。
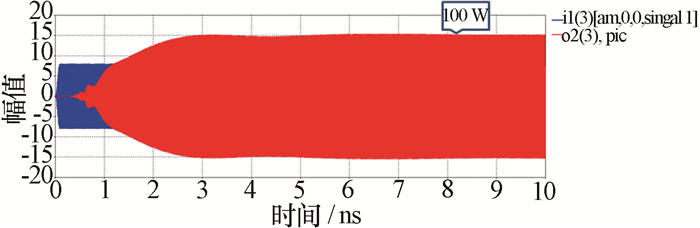
当输入功率为8 W时,输出功率约为50 W,增益为7.9 dB。此时TE30模式及其返波输出功率为5 mW,TE20模式及其返波输出功率不足1/1 000 mW,且没有振荡趋势,仿真结果较为稳定,低次模式竞争及返波振荡均得到了有效抑制。图 10为8 W输入时的输出信号与输入信号对比图,图中纵坐标的幅值平方除以2后为功率值,输入信号幅值为4,输出信号幅值为10。图中黑色信号为输出信号,红色信号为输入信号。
如图 11所示,当输入功率为32 W,幅值为8时,单段输出功率接近饱和,此时输出功率约为112.5 W,幅值为15且结果较为稳定,增益为5.46 dB,这是由于输出功率接近饱和所以增益有所降低。
2.3 两段电路输出结果
因此最终决定采用两段电路,每段电路为30个周期长度,中间使用2.5个周期长度的切断结构,两段电路的PIC仿真模型如图 12所示。
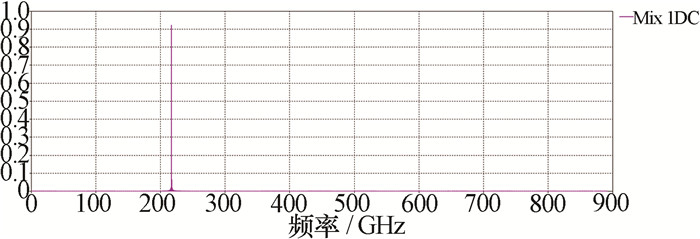
如图 13所示,当输入功率为1.125 W、幅值为1.5时,两段电路输出功率为103.5 W,输出信号幅值为14.3,此时增益为19.6 dB,TE10模式前向波输出功率为20 mW,返波功率为2.5 mW;TE20模式前向波输出功率为0.2 mW,返波功率不足1/1 000 mW,输出较为稳定。对输出信号进行傅里叶变换,得到信号的频谱图,如图 14所示,其频谱仅有217 GHz附近的峰值,频谱较为纯净。
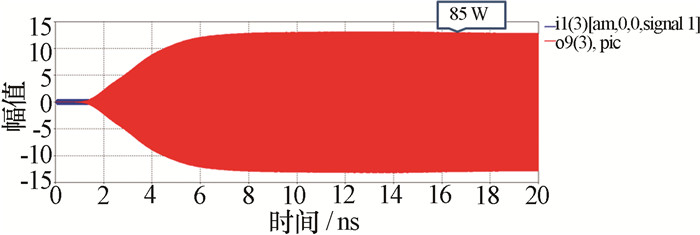
如图 15所示,其他条件均一致的情况下,继续增加电路段数,长度分别为1段30周期和3段15周期,输入功率为0.125 W,如图 16所示,此时饱和增益达到了28.3 dB,饱和输出功率为85 W,返波及低次模式功率不足10 mW,结果较为稳定。
在不断增加切断次数的过程中,可以看出,采用新结构的互作用电路的增益有很大的提升空间,这与冷测特性中的高耦合阻抗相印证。但在增益提升的过程中饱和输出功率在持续降低,本文认为产生该现象的原因在于新结构本身能产生很高增益,但由于过模行波管增益提高会导致返波振荡的产生,因此稳定工作的情况下增益受到了限制。而增加切断次数对返波振荡有着很强的抑制作用,切断次数越多,互作用电路工作更稳定,增益受到的限制也就越小,但是切断会产生额外的功率损耗,因此虽然多段电路的增益有所提升但饱和输出功率却在降低。
3. 结论
本文在传统交错双栅慢波结构的基础上进行改进,提出了一种适合在高次模式工作的新型结构。该结构的横向尺寸和电子注通道高度分别为同频段基模交错栅的3倍和2倍,在仅使用W波段附近的加工工艺情况下,能实现G波段的输出结果,同时更加适应大电流工作,且更大的尺寸有利于缓解慢波结构的散热问题。该结构在冷测特性上虽然一定程度上牺牲了带宽,但在工作点附近具有更高的耦合阻抗且获得了一些全新的特性,能有效抑制过模行波管的低次模式竞争及返波振荡等问题,且工作电压相对较低。在26 kV电压、两个150 mA电流的工作条件下,实现了217 GHz附近103.5 W的输出,且低次模式及返波抑制效果极佳。该结构工作在TE30模高次模式,由于TE30模式工作需要同时抑制TE10和TE20模式的返波振荡及模式竞争,有报道的成功使用TE30模式工作的成果极少,且都有一些限制,文中提出的结构对过模行波管的研究具有很大意义。
-
表 1 新结构参数

表 2 26 kV电压线交点处各模式频率及耦合阻抗
模式 10返波 20返波 10前向波 20返波 30工作点 谐波次数 -1 -1 -1 0 0 频率/GHz 101.00 117.00 129.50 171.00 217.32 耦合阻抗/Ω 0.37 0.60 5.20 2.57 15.60 -
[1] 窦好刚, 张亚斌, 杨景红. 行波管发射组件技术研究与实践[J]. 现代雷达, 2024, 46(11): 100-104 DOU H G, ZHANG Y B, YANG J H. A study and practice of transmiting module technology for travellingwave tube[J]. Modern Radar, 2024, 46(11): 100-104
[2] 杨金生, 纪焕丽, 孙然, 等. W波段4路平面集成行波管[J]. 微波学报, 2024, 40(6): 1-5 YANG J S, JI H L, SUN R, et al. W band 4-channel planar integrated traveling wave tube[J]. Journal of Microwaves, 2024, 40(6): 1-5
[3] ZHOU K C, FENG J J. Cold characteristics of overmoded ridge-and groove-loaded folded waveguides for high power travelling wave tubes[J]. IEEE Transactions on Plasma Science, 2021, 49(12): 4009-4016 DOI: 10.1109/TPS.2021.3127498
[4] 薛谦忠, 王瀚, 刘克刚. W波段新型带状注扩展互作用振荡器的设计[J]. 微波学报, 2023, 39(S1): 143-144 XUE Q Z, WANG H, LIU K G. Design of a W-band novel sheet-beam extended interaction oscillator[J]. Journal of Microwaves, 2023, 39(S1): 143-144
[5] ZHANG Z, RUAN C J. Design of a 220 GHz TE20 higher order mode SDVSWS TWT amplifier[C]// 2020 IEEE Asia-Pacific Microwave Conference(APMC). HongKong: IEEE Press, 2020: 646-648
[6] GEE A, SHIN Y M. Gain analysis of higher-order-mode amplification in a dielectric-implanted multi-beam traveling wave structure[J]. Physics of Plasmas, 2013, 20(7): 107-110 DOI: 10.1063/1.4818504
[7] TIAN Y, SHU G, Y. GONG Y, et al. Research on folded double-groove waveguide with two sheet beams operating on high-order TE20 mode for high-power terahertz TWT[J] IEEE Transactions on Electron Devices, 2022, 70(2): 830-834
[8] SHU G X, LIU G, QIAN Z F, et al. Microfabrication, and characterization of a subterahertz-band high-order overmoded double-staggered grating waveguide for multiple-sheet electron beam devices[J]. IEEE Transactions Electron Devices, 2021, 68(6): 3021-3027 http://ieeexplore.ieee.org/document/9424188
[9] REN J, SHU G, HE J, et al. Preliminarily design of a sub-terahertz high-order mode double-staggered grating waveguide for multiple-sheet electron beam traveling wave tubes[C]// IET Ph. D Candidates Academic Seminar (China) on Vacuum Electronics (PhASe-VE 2021), Online Conference. Beijing: IEEE Press, 2021: 27-29
[10] 刘英洲, 张长青, 潘攀, 等. 一维带状注行波管注波互作用快速计算程序[J]. 微波学报, 2024, 40(6): 14-21 LIU Y Z, ZHANG C Q, PAN P, et al. Large signal 1-D rapid beam-wave interaction simulation of sheet electron beam traveling wave tubes equivalent circuit analysis of staggered double-grating slow-wave structure[J]. Journal of Microwaves, 2024, 40(6): 14-21
[11] 李金磊, 罗积润, 樊宇. 交错双栅慢波结构的等效电路法研究[J]. 真空科学与技术学报, 2017, 37(5): 510-518 LI J L, LUO J R, FAN Y. Equivalent circuit analysis of staggered double-grating slow-wave structure[J]. Chinese Journal of Vacuum Science And. Technokogy, 2017, 37(5): 510-518
[12] 崔俊婷, 易红霞, 黄明光. 太赫兹波段光子晶体矩形栅慢波结构的对比研究[J]. 微波学报, 2016, 32(S2): 505-507 DOI: 10.13922/j.cnki.cjovst.2016.12.02 CUI J T, YI H X, HUANG M G. Study of THz photonic crystal grating rectangular slow-wave structure[J]. Journal of Microwaves, 2016, 32(S2): 505-507 DOI: 10.13922/j.cnki.cjovst.2016.12.02
[13] 高强, 闫敦豹, 袁乃昌, 等. 光子带隙结构在微带带通滤波器中的应用[J]. 微波学报, 2004, 20(3): 55-57 GAO Q, YAN D B, YUAN N C, et al. Application of photonic bandgap structure in microstrip bandpass filters[J]. Journal of Microwaves, 2004, 20(3): 55-57
[14] 王文祥. 微波工程技术[M]. 北京: 国防工业出版社, 2013 WANG W X. Microwave engineering techniques[M]. Beijing: National Defense Industry Press, 2013
[15] 杜英华, 蔡军, 张小青, 等. W波段行波管低电压小型化技术研究[J]. 微波学报, 2024, 40(6): 10-13 DU Y H, CAI J, ZHANG X Q, et al. Study on the low voltage and miniaturization technologies for W-band traveling wave tube[J]. Journal of Microwaves, 2024, 40(6): 10-13





 下载:
下载: